mlpack

BinarySpaceTree

The BinarySpaceTree class represents a generic multidimensional binary space partitioning tree. It is heavily templatized to control splitting behavior and other behaviors, and is the actual class underlying trees such as the KDTree. In general, the BinarySpaceTree class is not meant to be used directly, and instead one of the numerous variants should be used instead:

For users who want to use BinarySpaceTree directly or with custom behavior, the full class is still detailed in the subsections below. BinarySpaceTree supports the TreeType API and can be used with mlpack’s tree-based algorithms, although using custom behavior may require a template typedef.

🔗 See also

🔗 Template parameters

The BinarySpaceTree class takes five template parameters. The first three of these are required by the TreeType API (see also this more detailed section). The full signature of the class is:

template<typename DistanceType,
         typename StatisticType,
         typename MatType,
         template<typename BoundDistanceType,
                  typename BoundElemType,
                  typename...> class BoundType,
         template<typename SplitBoundType,
                  typename SplitMatType> class SplitType>
class BinarySpaceTree;

Note that the TreeType API requires trees to have only three template parameters. In order to use a BinarySpaceTree with its five template parameters with an mlpack algorithm that needs a TreeType, it is easiest to define a template typedef:

template<typename DistanceType, typename StatisticType, typename MatType>
using CustomTree = BinarySpaceTree<DistanceType, StatisticType, MatType,
    CustomBoundType, CustomSplitType>

Here, CustomBoundType and CustomSplitType are the desired bound and split strategy. This is the way that all BinarySpaceTree variants (such as KDTree) are defined.

🔗 Constructors

BinarySpaceTrees are efficiently constructed by permuting points in a dataset in a quicksort-like algorithm. However, this means that the ordering of points in the tree’s dataset (accessed with node.Dataset()) after construction may be different.

Notes:

🔗 Constructor parameters:

name type description default
data MatType Column-major matrix to build the tree on. Pass with std::move(data) to avoid copying the matrix. (N/A)
maxLeafSize size_t Maximum number of points to store in each leaf. 20
oldFromNew std::vector<size_t> Mappings from points in node.Dataset() to points in data. (N/A)
newFromOld std::vector<size_t> Mappings from points in data to points in node.Dataset(). (N/A)

🔗 Basic tree properties

Once a BinarySpaceTree object is constructed, various properties of the tree can be accessed or inspected. Many of these functions are required by the TreeType API.

🔗 Accessing members of a tree

See also the developer documentation for basic tree functionality in mlpack.

🔗 Accessing data held in a tree

🔗 Accessing computed bound quantities of a tree

The following quantities are cached for each node in a BinarySpaceTree, and so accessing them does not require any computation. In the documentation below, ElemType is the element type of the given MatType; e.g., if MatType is arma::mat, then ElemType is double.

Note: for more details on each bound quantity, see the developer documentation on bound quantities for trees.

🔗 Other functionality

🔗 Bounding distances with the tree

The primary use of trees in mlpack is bounding distances to points or other tree nodes. The following functions can be used for these tasks.

🔗 Tree traversals

Like every mlpack tree, the BinarySpaceTree class provides a single-tree and dual-tree traversal that can be paired with a RuleType class to implement a single-tree or dual-tree algorithm.

In addition to those two classes, which are required by the TreeType policy, an additional traverser is available:

🔗 BoundType

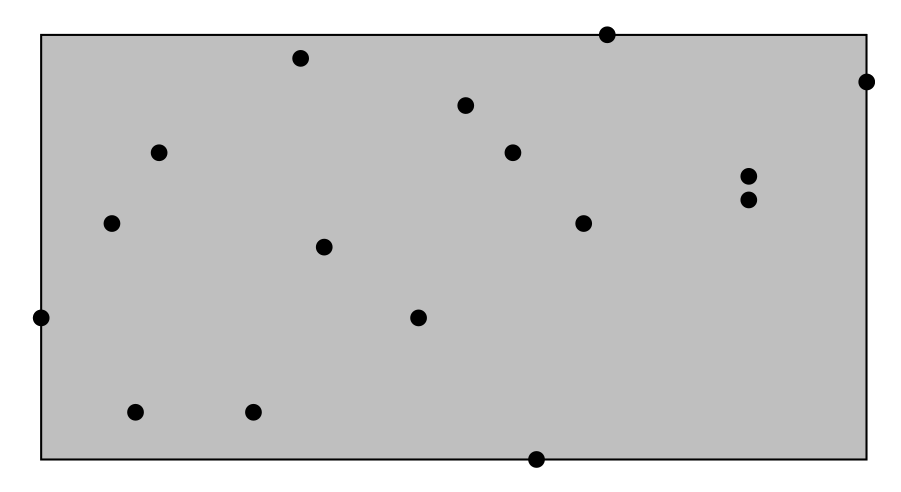
Each node in a BinarySpaceTree corresponds to some region in space that contains all of the descendant points in the node. This region is represented by the BoundType class. The use of different BoundTypes can mean different shapes for each node in the tree; for instance, the HRectBound class uses a hyperrectangle bound. An example HRectBound is shown below; the bound is the smallest rectangle that encloses all of the points.

hyperrectangle bound enclosing points

mlpack supplies several drop-in BoundType classes, and it is also possible to write a custom BoundType for use with BinarySpaceTree:

🔗 HRectBound

The HRectBound class represents a hyper-rectangle bound; that is, a rectangle-shaped bound in arbitrary dimensions (e.g. a “box”). An HRectBound can be used to perform a variety of distance-based bounding tasks.

HRectBound is used directly by the KDTree class.

Constructors

HRectBound allows configurable behavior via its two template parameters:

HRectBound<DistanceType, ElemType>

Different constructor forms can be used to specify different template parameters (and thus different bound behavior).

Note: these constructors provide an empty bound; be sure to grow the bound or directly modify the bound before using it!

Accessing and modifying properties of the bound

The individual bounds associated with each dimension of an HRectBound can be accessed and modified.

Note: if a custom ElemType was specified in the constructor, then:

Growing and shrinking the bound

The HRectBound uses the logical |= and &= operators to perform set operations with data points or other bounds.

Notes:

Bounding distances to other objects

Once an HRectBound has been successfully created and set to the desired bounding hyperrectangle, there are a number of functions that can bound the distance between an HRectBound and other objects.

Note: if a custom DistanceType and ElemType were specified in the constructor, then all distances will be computed with respect to the specified DistanceType and all return values will either be ElemType or RangeType<ElemType> (except for Contains(), which will still return a bool).

Example usage

// Create a bound that is the unit cube in 3 dimensions, by setting the values
// manually.  The bounding range for all three dimensions is [0.0, 1.0].
mlpack::HRectBound b(3);
b[0] = mlpack::Range(0.0, 1.0);
b[1].Lo() = 0.0;
b[1].Hi() = 1.0;
b[2] = b[1];
// The minimum width is not correct if we modify bound dimensions manually, so
// we have to recompute it.
b.RecomputeMinWidth();

std::cout << "Bounding box created manually:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b[i].Lo() << ", " << b[i].Hi()
      << "]." << std::endl;
}

// Create a small dataset of 5 points, and then create a bound that contains all
// of those points.
arma::mat dataset(3, 5);
dataset.col(0) = arma::vec("2.0 2.0 2.0");
dataset.col(1) = arma::vec("2.5 2.5 2.5");
dataset.col(2) = arma::vec("3.0 2.0 3.0");
dataset.col(3) = arma::vec("2.0 3.0 2.0");
dataset.col(4) = arma::vec("3.0 3.0 3.0");

// The bounding box of `dataset` is [2.0, 3.0] in all three dimensions.
mlpack::HRectBound b2(3);
b2 |= dataset;

std::cout << "Bounding box created on dataset:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b2[i].Lo() << ", " << b2[i].Hi()
      << "]." << std::endl;
}

// Create a new bound that is the union of the two bounds.
mlpack::HRectBound b3 = b;
b3 |= b2;

std::cout << "Union-ed bounding box:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b3[i].Lo() << ", " << b3[i].Hi()
      << "]." << std::endl;
}

// Create a new bound that is the intersection of the two bounds (this will be
// empty!).
mlpack::HRectBound b4 = (b & b2);

std::cout << "Intersection bounding box:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b4[i].Lo() << ", " << b4[i].Hi()
      << "].";
  if (b4[i].Hi() < b4[i].Lo())
    std::cout << " (Empty!)";
  std::cout << std::endl;
}

// Print statistics about the union bound and intersection bound.
std::cout << "Union-ed bound details:" << std::endl;
std::cout << " - Dimensionality: " << b3.Dim() << "." << std::endl;
std::cout << " - Minimum width: " << b3.MinWidth() << "." << std::endl;
std::cout << " - Diameter: " << b3.Diameter() << "." << std::endl;
std::cout << " - Volume: " << b3.Volume() << "." << std::endl;
arma::vec center;
b3.Center(center);
std::cout << " - Center: " << center.t();
std::cout << std::endl;

std::cout << "Intersection bound details:" << std::endl;
std::cout << " - Dimensionality: " << b4.Dim() << "." << std::endl;
std::cout << " - Minimum width: " << b4.MinWidth() << "." << std::endl;
std::cout << " - Diameter: " << b4.Diameter() << "." << std::endl;
std::cout << " - Volume: " << b4.Volume() << "." << std::endl;
b4.Center(center);
std::cout << " - Center: " << center.t();
std::cout << std::endl;

// Compute the minimum distance between a point inside the unit cube and the
// unit cube bound.
const double d1 = b.MinDistance(arma::vec("0.5 0.5 0.5"));
std::cout << "Minimum distance between unit cube bound and [0.5, 0.5, 0.5]: "
    << d1 << "." << std::endl;

// Use Contains().  In this case, the 'else' will be taken.
if (b.Contains(arma::vec("1.5 1.5 1.5")))
  std::cout << "Unit cube bound contains [1.5, 1.5, 1.5]." << std::endl;
else
  std::cout << "Unit cube does not contain [1.5, 1.5, 1.5]." << std::endl;
std::cout << std::endl;

// Compute the maximum distance between a point inside the unit cube and the
// unit cube bound.
const double d2 = b.MaxDistance(arma::vec("0.5 0.5 0.5"));
std::cout << "Maximum distance between unit cube bound and [0.5, 0.5, 0.5]: "
    << d2 << "." << std::endl;

// Compute the minimum and maximum distances between the unit cube bound and the
// bound built on data points.
const mlpack::Range r = b.RangeDistance(b2);
std::cout << "Distances between unit cube bound and dataset bound: [" << r.Lo()
    << ", " << r.Hi() << "]." << std::endl;

// Create a random bound.
mlpack::HRectBound br(3);
for (size_t i = 0; i < 3; ++i)
  br[i] = mlpack::Range(mlpack::Random(), mlpack::Random() + 1);
std::cout << "Randomly created bound:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << br[i].Lo() << ", " << br[i].Hi()
      << "]." << std::endl;
}

// Compute the overlap of various bounds.
const double o1 = b.Overlap(b2); // This will be 0: the bounds don't overlap.
const double o2 = b.Overlap(b3); // This will be 1; b3 fully overlaps b, and
                                 // the volume of b is 1 (it is the unit cube).
const double o3 = br.Overlap(b); // br and b do not fully overlap.
std::cout << "Overlap of unit cube and data bound: " << o1 << "." << std::endl;
std::cout << "Overlap of unit cube and union bound: " << o2 << "." << std::endl;
std::cout << "Overlap of unit cube and random bound: " << o3 << "."
    << std::endl;

// Create a bound using the Manhattan (L1) distance and compute the minimum and
// maximum distance to a point.
mlpack::HRectBound<mlpack::ManhattanDistance> mb(3);
mb |= dataset; // This will set the bound to [2.0, 3.0] in every dimension.
const mlpack::Range r2 = mb.RangeDistance(arma::vec("1.5 1.5 4.0"));
std::cout << "Distance between Manhattan distance HRectBound and "
    << "[1.5, 1.5, 4.0]: [" << r2.Lo() << ", " << r2.Hi() << "]." << std::endl;

// Create a bound using the Chebyshev (L-inf) distance, using random 32-bit
// floating point elements, and compute the minimum and maximum distance to a
// point.
arma::fmat floatData(3, 25, arma::fill::randu);
mlpack::HRectBound<mlpack::ChebyshevDistance, float> cb;
cb |= floatData;
// Note the use of arma::fvec to represent a point, since ElemType is float.
const mlpack::RangeType<float> r3 = cb.RangeDistance(arma::fvec("1.5 1.5 4.0"));
std::cout << "Distance between Chebyshev distance HRectBound and "
    << "[1.5, 1.5, 4.0]: [" << r3.Lo() << ", " << r3.Hi() << "]." << std::endl;

🔗 BallBound

The BallBound class represents a ball with a center and a radius. A BallBound can be used to perform a variety of distance-based bounding tasks.

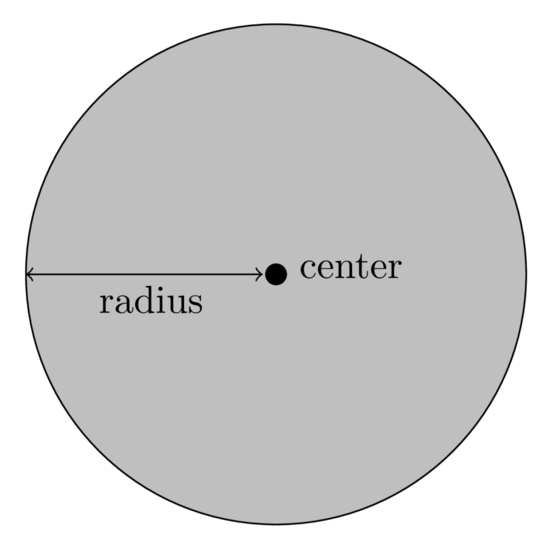
ball bound

BallBound is used directly by the BallTree class.

Constructors

BallBound allows configurable behavior via its three template parameters:

BallBound<DistanceType, ElemType, VecType>

The three template parameters are described below:

Different constructor forms can be used to specify different template parameters (and thus different bound behavior).

Note: these constructors provide an empty bound; be sure to grow the bound or directly modify the bound before using it!

Accessing and modifying properties of the bound

The properties of the BallBound can be directly accessed and modified.

Note: if a custom ElemType and/or VecType were specified in the constructor, then:

Growing the bound

The BallBound uses the logical |= to grow the bound to include points or other BallBounds.

Bounding distances to other objects

Once a BallBound has been successfully created and set to the desired bounding ball, there are a number of functions that can bound the distance between a BallBound and other objects.

Note: if a custom DistanceType, ElemType, or VecType were specified in the constructor, then:

Example usage

// Create a bound that is the unit ball in 3 dimensions, by setting the center
// and radius in the constructor.
mlpack::BallBound b(1.0, arma::vec(3, arma::fill::zeros));

std::cout << "Bounding ball created manually:" << std::endl;
std::cout << " - Center: " << b.Center().t();
std::cout << " - Radius: " << b.Radius() << "." << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << " range: [" << b[i].Lo() << ", "
      << b[i].Hi() << "]." << std::endl;
}

// Create a small dataset of 5 points, and then create a bound that contains all
// of those points.
arma::mat dataset(3, 5);
dataset.col(0) = arma::vec("2.0 2.0 2.0");
dataset.col(1) = arma::vec("2.5 2.5 2.5");
dataset.col(2) = arma::vec("3.0 2.0 3.0");
dataset.col(3) = arma::vec("2.0 3.0 2.0");
dataset.col(4) = arma::vec("3.0 3.0 3.0");

// The bounding ball will be computed using Jack Ritter's algorithm.
mlpack::BallBound b2(3);
b2 |= dataset;

std::cout << "Bounding ball created on dataset:" << std::endl;
std::cout << " - Center: " << b2.Center().t();
std::cout << " - Radius: " << b2.Radius() << "." << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b2[i].Lo() << ", " << b2[i].Hi()
      << "]." << std::endl;
}

// Compute the minimum distance between a point inside the unit ball and the
// unit ball bound.
const double d1 = b.MinDistance(arma::vec("0.5 0.5 0.5"));
std::cout << "Minimum distance between unit ball bound and [0.5, 0.5, 0.5]: "
    << d1 << "." << std::endl;

// Use Contains().  In this case, the 'else' will be taken.
if (b.Contains(arma::vec("1.5 1.5 1.5")))
  std::cout << "Unit ball bound contains [1.5, 1.5, 1.5]." << std::endl;
else
  std::cout << "Unit ball does not contain [1.5, 1.5, 1.5]." << std::endl;
std::cout << std::endl;

// Compute the maximum distance between a point inside the unit ball and the
// unit ball bound.
const double d2 = b.MaxDistance(arma::vec("0.5 0.5 0.5"));
std::cout << "Maximum distance between unit ball bound and [0.5, 0.5, 0.5]: "
    << d2 << "." << std::endl;

// Compute the minimum and maximum distances between the unit ball bound and the
// bound built on data points.
const mlpack::Range r = b.RangeDistance(b2);
std::cout << "Distances between unit ball bound and dataset bound: [" << r.Lo()
    << ", " << r.Hi() << "]." << std::endl;

// Create a random bound with radius between 1 and 2 and random center.
mlpack::BallBound br(3);
br.Radius() = 1.0 + mlpack::Random();
br.Center() = arma::randu<arma::vec>(3);
std::cout << "Randomly created bound:" << std::endl;
std::cout << " - Center: " << br.Center().t();
std::cout << " - Radius: " << br.Radius() << "." << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << br[i].Lo() << ", " << br[i].Hi()
      << "]." << std::endl;
}

// Create a bound using the Manhattan (L1) distance and compute the minimum and
// maximum distance to a point.
mlpack::BallBound<mlpack::ManhattanDistance> mb(3);
mb |= dataset; // Expand the bound to include the points in the dataset.
const mlpack::Range r2 = mb.RangeDistance(arma::vec("1.5 1.5 4.0"));
std::cout << "Distance between Manhattan distance BallBound and "
    << "[1.5, 1.5, 4.0]: [" << r2.Lo() << ", " << r2.Hi() << "]." << std::endl;

// Create a bound using the Chebyshev (L-inf) distance, using random 32-bit
// floating point elements, and compute the minimum and maximum distance to a
// point.
arma::fmat floatData(3, 25, arma::fill::randu);
mlpack::BallBound<mlpack::ChebyshevDistance, float> cb;
cb |= floatData; // Expand the bound to include the points in the dataset.
// Note the use of arma::fvec to represent a point, since ElemType is float.
const mlpack::RangeType<float> r3 = cb.RangeDistance(arma::fvec("1.5 1.5 4.0"));
std::cout << "Distance between Chebyshev distance BallBound and "
    << "[1.5, 1.5, 4.0]: [" << r3.Lo() << ", " << r3.Hi() << "]." << std::endl;

🔗 HollowBallBound

The HollowBallBound class represents a bounding shape that is an arbitrary-dimensional ball bound with another smaller ball subtracted from its inside. A HollowBallBound consists of a center point, an outer radius, and a secondary center point and inner radius. An example HollowBallBound is shown below in two dimensions; shaded area represents area held within the bound.

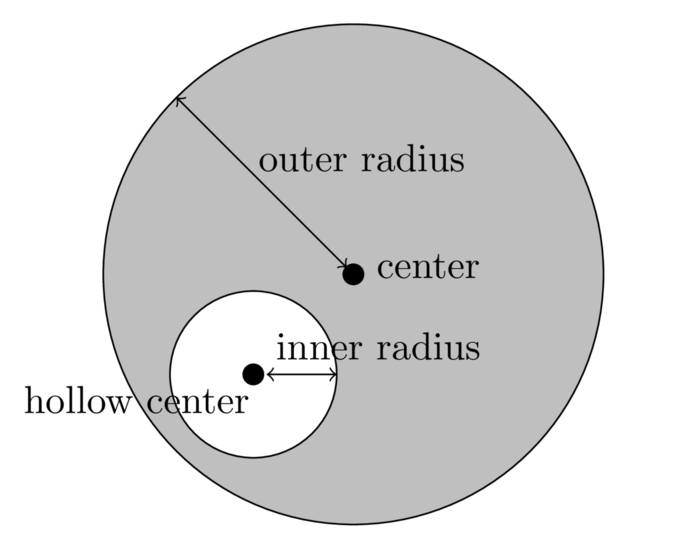
hollow ball bound

HollowBallBound is used directly by the VPTree class.

Constructors

HollowBallBound allows configurable behavior via its two template parameters:

HollowBallBound<DistanceType, ElemType>

Different constructor forms can be used to specify different template parameters (and thus different bound behavior).

Note: these constructors provide an empty bound; be sure to grow the bound or directly modify the bound before using it!

Accessing and modifying properties of the bound

The individual bounds associated with each dimension of a HollowBallBound can be accessed and modified.

Note: if a custom ElemType was specified in the constructor, then:

Growing the bound

The HollowBallBound uses the logical |= to grow the bound to include points or other bounds.

Notes:

Bounding distances to other objects

Once a HollowBallBound has been successfully created and set to the desired bounding balls, there are a number of functions that can bound the distance between a HollowBallBound and other objects.

Note: if a custom DistanceType and ElemType were specified in the constructor, then all distances will be computed with respect to the specified DistanceType and all return values will either be ElemType or RangeType<ElemType> (except for Contains(), which will still return a bool).

Example usage

// Create a hollow ball bound in 3 dimensions whose outer ball is the unit ball
// and whose inner ball is the ball with radius 0.5 centered at the origin.
// The bounding range for all three dimensions is [0.0, 1.0].
mlpack::HollowBallBound b(0.5, 1.0, arma::vec(3));

std::cout << "Hollow unit ball bound created manually:" << std::endl;
std::cout << " - Center: " << b.Center().t();
std::cout << " - Outer radius: " << b.OuterRadius() << "." << std::endl;
std::cout << " - Hollow center: " << b.HollowCenter().t();
std::cout << " - Inner radius: " << b.InnerRadius() << "." << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << " extents: [" << b[i].Lo() << ", "
      << b[i].Hi() << "]." << std::endl;
}
std::cout << std::endl;

// Create a small dataset of 5 points.
arma::mat dataset(3, 5);
dataset.col(0) = arma::vec("2.0 2.0 2.0");
dataset.col(1) = arma::vec("2.5 2.5 2.5");
dataset.col(2) = arma::vec("3.0 2.0 3.0");
dataset.col(3) = arma::vec("2.0 3.0 2.0");
dataset.col(4) = arma::vec("3.0 3.0 3.0");

// If we simply build a HollowBallBound to enclose those points, the hollow part
// of the ball is unmodified and remains empty.
mlpack::HollowBallBound b2(3);
b2 |= dataset;
std::cout << "Hollow ball bound on points with only `operator|=()`:"
    << std::endl;
std::cout << " - Center: " << b2.Center().t();
std::cout << " - Outer radius: " << b2.OuterRadius() << "." << std::endl;
std::cout << " - Hollow center: " << b2.HollowCenter().t();
std::cout << " - Inner radius: " << b2.InnerRadius() << "." << std::endl;
std::cout << std::endl;

// On the other hand, if we initialize a HollowBallBound to a non-empty bound,
// then `operator|=()` will shrink the hollow ball as necessary.
//
// We initialize this ball bound to a "slice" with radii [3.6, 3.7].
mlpack::HollowBallBound b3(3.6, 3.7, arma::vec(3));
b3 |= dataset;
std::cout << "Hollow ball bound on points with pre-initialization and "
    << "`operator|=()`:" << std::endl;
std::cout << " - Center: " << b3.Center().t();
std::cout << " - Outer radius: " << b3.OuterRadius() << "." << std::endl;
std::cout << " - Hollow center: " << b3.HollowCenter().t();
std::cout << " - Inner radius: " << b3.InnerRadius() << "." << std::endl;
std::cout << std::endl;

// Manually create a hollow ball bound whose hollow center is different than the
// outer ball's center.
mlpack::HollowBallBound b4(3);
b4.OuterRadius() = 3.0;
b4.InnerRadius() = 1.5;
b4.Center() = arma::vec(3);
b4.HollowCenter() = arma::vec("1.0 1.0 1.0");

// Compute the minimum distance between a point inside the hollow unit ball's
// outer ball.
const double d1 = b.MinDistance(arma::vec("0.9 0.9 0.9"));
std::cout << "Minimum distance between hollow unit ball bound and [0.9, 0.9, "
    << "0.9]: " << d1 << "." << std::endl;

// Compute the minimum distance between a point inside the hollow unit ball's
// inner ball (so the point is not contained in the bound---it is within the
// hollow section).
const double d2 = b.MinDistance(arma::vec("0.0 0.0 0.0"));
std::cout << "Minimum distance between hollow unit ball bound and [0.0, 0.0, "
    << "0.0]: " << d2 << "." << std::endl;
std::cout << std::endl;

// Use Contains().  In this case, the 'else' will be taken.
if (b.Contains(arma::vec("1.5 1.5 1.5")))
{
  std::cout << "Hollow unit ball bound contains [1.5, 1.5, 1.5]." << std::endl;
}
else
{
  std::cout << "Hollow unit ball bound does not contain [1.5, 1.5, 1.5]."
      << std::endl;
}
std::cout << std::endl;

// Compute the maximum distance between a point inside the unit ball and the
// unit hollow ball bound.
const double d3 = b4.MaxDistance(arma::vec("0.1 0.1 0.1"));
std::cout << "Maximum distance between hollow unit ball bound and [0.1, 0.1, "
    << "0.1]: " << d3 << "." << std::endl;

// Compute the minimum and maximum distances between the hollow unit ball bound
// and the bound built on data points.
const mlpack::Range r = b.RangeDistance(b3);
std::cout << "Distances between hollow unit ball bound and second hollow "
    << "dataset bound: [" << r.Lo() << ", " << r.Hi() << "]." << std::endl;

// Create a bound using the Manhattan (L1) distance and compute the minimum and
// maximum distance to a point.
mlpack::HollowBallBound<mlpack::ManhattanDistance> mb(2.0, 5.0, arma::vec(3));
const mlpack::Range r2 = mb.RangeDistance(arma::vec("1.5 1.5 4.0"));
std::cout << "Distance between Manhattan distance HollowBallBound and "
    << "[1.5, 1.5, 4.0]: [" << r2.Lo() << ", " << r2.Hi() << "]." << std::endl;

// Create a bound using the Chebyshev (L-inf) distance, using random 32-bit
// floating point elements, and compute the minimum and maximum distance to a
// point.
arma::fmat floatData(3, 25, arma::fill::randu);
mlpack::HollowBallBound<mlpack::ChebyshevDistance, float> cb;
cb |= floatData;
// Note the use of arma::fvec to represent a point, since ElemType is float.
const mlpack::RangeType<float> r3 = cb.RangeDistance(arma::fvec("1.5 1.5 4.0"));
std::cout << "Distance between Chebyshev distance HollowBallBound and "
    << "[1.5, 1.5, 4.0]: [" << r3.Lo() << ", " << r3.Hi() << "]." << std::endl;

🔗 CellBound

The CellBound class represents a bound made up of a contiguous subregion of a hyperrectangle. Suppose that the region represented by a hyperrectangle was linearized and then ordered with Z-ordering. Under this scheme, a CellBound can be represented as containing all points whose linearization falls between a “start address” and an “end address”. A simple depiction of a 2-dimensional CellBound is shown below.

cellbound 1 with 3-bit addresses

In the example above, p_1 represents the point that is the “start address”, and p_2 represents the point that is the “end address”; any points with address in between those (e.g. the shaded region) are contained in the CellBound.

CellBound is used directly by the UBTree (universal B-tree) class.

Addressing in a CellBound

In a CellBound, each point is mapped to an ordered “address” that indicates its position in the bound using Z-ordering (also called Morton ordering). The mathematical details of this mapping are described in the UB-tree paper; although mlpack uses a slightly modified implementation, the general idea is the same.

The following two functions can be used to convert to and from linearized addresses:

Constructors

CellBound allows configurable behavior via its two template parameters:

CellBound<DistanceType, ElemType>

Different constructor forms can be used to specify different template parameters (and thus different bound behavior).

Note: these constructors provide an empty bound; be sure to grow the bound before using it!

Accessing properties of the bound

The individual bounds associated with each dimension of a CellBound can be accessed, but should not be directly modified—see growing the bound for ways to grow a CellBound.

Note: if a custom ElemType was specified in the constructor, then:

Growing the bound

The CellBound uses the logical |= operator to grow the bound to contain sets of points or other bounds.

Notes:

Bounding distances to other objects

Once a CellBound has been successfully created and set to the desired subset of its bounding hyperrectangle, there are a number of functions that can bound the distance between a CellBound and other objects.

Note: if a custom DistanceType and ElemType were specified in the constructor, then all distances will be computed with respect to the specified DistanceType and all return values will either be ElemType or RangeType<ElemType> (except for Contains(), which will still return a bool).

Example usage

// Create a random dataset of 50 points in 3 dimensions.
arma::mat dataset(3, 50, arma::fill::randu);

// Now create a CellBound that contains those points via the |= operator.
mlpack::CellBound b(3);
b |= dataset;
b.UpdateAddressBounds(dataset);

std::cout << "Outer bounding box of CellBound:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b[i].Lo() << ", " << b[i].Hi()
      << "]." << std::endl;
}

// Create another random dataset, but shifted to fit in a box ranging from
// [2, 2, 2] to [3, 3, 3].
arma::mat dataset2(3, 50, arma::fill::randu);
dataset2 += 2.0;
mlpack::CellBound b2(3);
b2 |= dataset2;
b2.UpdateAddressBounds(dataset2);

std::cout << "Outer bounding box of second CellBound:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b2[i].Lo() << ", " << b2[i].Hi()
      << "]." << std::endl;
}

// Compute union of two CellBounds.
mlpack::CellBound b3(3);
b3 |= b;
b3 |= b2;

std::cout << "Outer bounding box of union CellBound:" << std::endl;
for (size_t i = 0; i < 3; ++i)
{
  std::cout << " - Dimension " << i << ": [" << b3[i].Lo() << ", " << b3[i].Hi()
      << "]." << std::endl;
}

// Print statistics about the union bound.
std::cout << "Union bound details:" << std::endl;
std::cout << " - Dimensionality: " << b3.Dim() << "." << std::endl;
std::cout << " - Minimum width: " << b3.MinWidth() << "." << std::endl;
std::cout << " - Diameter: " << b3.Diameter() << "." << std::endl;
arma::vec center;
b3.Center(center);
std::cout << " - Center: " << center.t();
std::cout << std::endl;

// Compute the minimum distance between a point and the first two bounds.
const double d1 = b.MinDistance(arma::vec("1.5 1.5 1.5"));
const double d2 = b2.MinDistance(arma::vec("1.5 1.5 1.5"));
std::cout << "Minimum distance between first bound and [1.5, 1.5, 1.5]:  "
    << d1 << "." << std::endl;
std::cout << "Minimum distance between second bound and [1.5, 1.5, 1.5]: "
    << d2 << "." << std::endl;

// Use Contains().  In this case, the 'else' will be taken.
if (b.Contains(arma::vec("1.5 1.5 1.5")))
  std::cout << "First bound contains [1.5, 1.5, 1.5]." << std::endl;
else
  std::cout << "First bound does not contain [1.5, 1.5, 1.5]." << std::endl;
std::cout << std::endl;

// Compute the maximum distance between a point inside the unit cube and the
// first bound.
const double d3 = b.MaxDistance(arma::vec("0.5 0.5 0.5"));
std::cout << "Maximum distance between first bound and [0.5, 0.5, 0.5]: " << d2
    << "." << std::endl;

// Compute the minimum and maximum distances between first and second bounds.
const mlpack::Range r = b.RangeDistance(b2);
std::cout << "Distances between first bound and second bound: [" << r.Lo()
    << ", " << r.Hi() << "]." << std::endl;

// Create a bound using the Manhattan (L1) distance and compute the minimum and
// maximum distance to a point.
mlpack::CellBound<mlpack::ManhattanDistance> mb(3);
mb |= dataset;
mb.UpdateAddressBounds(dataset);
const mlpack::Range r2 = mb.RangeDistance(arma::vec("1.5 1.5 4.0"));
std::cout << "Distance between Manhattan distance CellBound and "
    << "[1.5, 1.5, 4.0]: [" << r2.Lo() << ", " << r2.Hi() << "]." << std::endl;

// Create a bound using the Chebyshev (L-inf) distance, using random 32-bit
// floating point elements, and compute the minimum and maximum distance to a
// point.
arma::fmat floatData(3, 25, arma::fill::randu);
mlpack::CellBound<mlpack::ChebyshevDistance, float> cb;
cb |= floatData; // This will set the bound to [2.0, 3.0] in every dimension.
cb.UpdateAddressBounds(floatData);
// Note the use of arma::fvec to represent a point, since ElemType is float.
const mlpack::RangeType<float> r3 = cb.RangeDistance(arma::fvec("1.5 1.5 4.0"));
std::cout << "Distance between Chebyshev distance CellBound and "
    << "[1.5, 1.5, 4.0]: [" << r3.Lo() << ", " << r3.Hi() << "]." << std::endl;

🔗 Custom BoundTypes

The BinarySpaceTree class allows an arbitrary BoundType template parameter to be specified for custom behavior. By default, this is HRectBound (a hyper-rectangle bound), but it is also possible to implement a custom BoundType. Any custom BoundType class must implement the following functions:

// NOTE: the custom BoundType class must take at least two template parameters.
template<typename DistanceType, typename ElemType>
class BoundType
{
 public:
  // A default constructor must be available.
  BoundType();

  // Initialize the bound to an empty bound in the given dimensionality.
  BoundType(const size_t dimensionality);

  // A copy and move constructor must be available.  (If your class is simple,
  // you can generally omit this and use the default-generated versions, which
  // are commented out below.)
  BoundType(const BoundType& other);
  BoundType(BoundType&& other);

  // BoundType(const BoundType& other) = default;
  // BoundType(BoundType&& other) = default;

  // Return the minimum and maximum ranges of the bound in the given dimension.
  mlpack::RangeType<ElemType> operator[](const size_t dim) const;

  // Return the longest possible distance between two points contained in the
  // bound.  (Examples: for a ball bound, this is just the regular diameter.
  // For a rectangle bound, this is the length of the longest diagonal.)
  ElemType Diameter() const;

  // Return the minimum width of the bound in any dimension.
  ElemType MinWidth() const;

  // Return the DistanceType object that this bound uses for distance
  // calculations.
  DistanceType& Distance();

  // Expand the bound so that it includes all of the data points in `points`.
  // `points` will be a matrix type whose element type matches `ElemType`.
  template<typename MatType>
  BoundType& operator|=(const MatType& points);

  // Compute the minimum possible distance between the given point and the
  // bound.  `VecType` will be a single column vector with element type that
  // matches `ElemType`.
  template<typename VecType>
  ElemType MinDistance(const VecType& point) const;

  // Compute the minimum possible distance between this bound and the given
  // other bound.
  ElemType MinDistance(const BoundType& other) const;

  // Compute the maximum possible distance between the given point and the
  // bound.  `VecType` will be a single column vector with element type that
  // matches `ElemType`.
  template<typename VecType>
  ElemType MaxDistance(const VecType& point) const;

  // Compute the maximum possible distance between this bound and the given
  // other bound.
  ElemType MaxDistance(const BoundType& other) const;

  // Compute the minimum and maximum distances between the given point and the
  // bound, returning them in a Range object.  `VecType` will be a single column
  // vector with element type that matches `ElemType`.
  template<typename VecType>
  mlpack::RangeType<ElemType> RangeDistance(const VecType& point) const;

  // Compute the minimum and maximum distances between this bound and the given
  // other bound, returning them in a Range object.
  mlpack::RangeType<ElemType> RangeDistance(const BoundType& other) const;

  // Compute the center of the bound and store it into the given `center`
  // vector.
  void Center(arma::Col<ElemType>& center);

  // Serialize the bound to disk using the cereal library.
  template<typename Archive>
  void serialize(Archive& ar, const uint32_t version);
};

Behavior of some aspects of the BinarySpaceTree depend on the traits of a particular bound. Optionally, you may define an mlpack::BoundTraits specialization for your bound type, of the following form:

// Replace `BoundType` below with the name of the custom class.
template<typename DistanceType, typename ElemType>
struct mlpack::BoundTraits<BoundType<DistanceType, ElemType>>
{
  //! If true, then the bounds for each dimension are tight.  If false, then the
  //! bounds for each dimension may be looser than the range of all points held
  //! in the bound.  This defaults to false if the struct is not defined.
  static const bool HasTightBounds = false;
};

Note that if a custom SplitType is being used, the custom BoundType will also have to implement any functions required by the custom SplitType. In addition, custom RuleTypes used with tree traversals may have additional requirements on the BoundType; the functions listed above are merely the minimum required to use a BoundType with a BinarySpaceTree.

🔗 StatisticType

Each node in a BinarySpaceTree holds an instance of the StatisticType class. This class can be used to store additional bounding information or other cached quantities that a BinarySpaceTree does not already compute.

mlpack provides a few existing StatisticType classes, and a custom StatisticType can also be easily implemented:

Note: this section is still under construction—not all statistic types are documented yet.

🔗 EmptyStatistic

The EmptyStatistic class is an empty placeholder class that is used as the default StatisticType template parameter for mlpack trees.

The class does not hold any members and provides no functionality. See the implementation.

🔗 Custom StatisticTypes

A custom StatisticType is trivial to implement. Only a default constructor and a constructor taking a BinarySpaceTree is necessary.

class CustomStatistic
{
 public:
  // Default constructor required by the StatisticType policy.
  CustomStatistic();

  // Construct a CustomStatistic for the given fully-constructed
  // `BinarySpaceTree` node.  Here we have templatized the tree type to make it
  // easy to handle any type of `BinarySpaceTree`.
  template<typename TreeType>
  StatisticType(TreeType& node);

  //
  // Adding any additional precomputed bound quantities can be done; these
  // quantities should be computed in the constructor.  They can then be
  // accessed from the tree with `node.Stat()`.
  //
};

Example: suppose we wanted to know, for each node, the exact time at which it was created. A StatisticType could be created that has a std::time_t member, whose value is computed in the constructor.

🔗 SplitType

The SplitType template parameter controls the algorithm used to split each node of a BinarySpaceTree while building. The splitting strategy used can be entirely arbitrary—the SplitType only needs to specify whether a node should be split, and if so, which points should go to the left child, and which should go to the right child.

mlpack provides several drop-in choices for SplitType, and it is also possible to write a fully custom split:

🔗 MidpointSplit

The MidpointSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the default strategy for splitting KDTrees.

The splitting strategy for the MidpointSplit class is, given a set of points:

For implementation details, see the source code.

🔗 MeanSplit

The MeanSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the splitting strategy used by the MeanSplitKDTree class.

The splitting strategy for the MeanSplit class is, given a set of points:

In practice, the MeanSplit splitting strategy often results in a tree with fewer leaf nodes than MidpointSplit, because each split is more likely to be balanced. However, counterintuitively, a more balanced tree can be worse for search tasks like nearest neighbor search, because unbalanced nodes are more easily pruned away during search. In general, using MidpointSplit for nearest neighbor search is 20-80% faster, but this is not true for every dataset or task.

For implementation details, see the source code.

🔗 VantagePointSplit

The VantagePointSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the default strategy for splitting VPTrees, and is detailed in the paper. Due to the nature of the split, VantagePointSplit should always be used with the HollowBallBound.

The splitting strategy for the VantagePointSplit class is, given a set of points:

The VantagePointSplit class has three template parameters:

VantagePointSplit<BoundType, MatType, MaxNumSamples = 100>

If a custom number of samples S is desired, the easiest way to specify is via a template typedef:

template<typename BoundType, typename MatType>
using MyVantagePointSplit = VantagePointSplit<BoundType, MatType, S>;

Then, MyVantagePointSplit can be used directly with BinarySpaceTree as a SplitType.

For implementation details, see the source code.

🔗 RPTreeMeanSplit

The RPTreeMeanSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the splitting strategy used by the RPTree class, and uses a random projection to split points. The general idea is described in the paper by Dasgupta and Freund, as the RPTree-Mean version of the ChooseRule() function.

The splitting strategy for the RPTreeMeanSplit class is, given a set of points:

The implementation strategy differs slightly from the RPTree-Mean version in the paper: instead of computing the true average pairwise distance between all points, a sample of 100 points is used.

For implementation details, see the source code.

🔗 RPTreeMaxSplit

The RPTreeMaxSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the splitting strategy used by the MaxRPTree class, and uses a random projection to split points. The general idea is described in the paper by Dasgupta and Freund, as the RPTree-Max version of the ChooseRule() function.

The splitting strategy for the RPTreeMaxSplit class is, given a set of points,

The implementation strategy differs slightly from the RPTree-Max version in the paper: instead of computing the median on all points, a sample of 100 points is used.

For implementation details, see the source code.

🔗 UBTreeSplit

The UBTreeSplit class is a splitting strategy that can be used by BinarySpaceTree. It is the splitting strategy used by theUBTree class (the universal B-tree), and it requires that the BoundType being used is CellBound.

The splitting strategy for the UBTreeSplit class is simple: with each point mapped to its corresponding linearized address, those points with address less than the median address go to the left child; other points go to the right child.

For implementation details, see the source code.

🔗 Custom SplitTypes

Custom split strategies for a binary space tree can be implemented via the SplitType template parameter. By default, the MidpointSplit splitting strategy is used, but it is also possible to implement and use a custom SplitType. Any custom SplitType class must implement the following signature:

// NOTE: the custom SplitType class must take two template parameters.
template<typename BoundType, typename ElemType>
class SplitType
{
 public:
  // The SplitType class must provide a SplitInfo struct that will contain the
  // information necessary to perform a split.  There are no required members
  // here; the BinarySpaceTree class merely passes these around in the
  // SplitNode() and PerformSplit() functions (see below).
  struct SplitInfo { };

  // Given that a node contains the points
  // `data.cols(begin, begin + count - 1)`, determine whether the node should be
  // split.  If so, `true` should be returned and `splitInfo` should be set with
  // the necessary information so that `PerformSplit()` can actually perform the
  // split.
  //
  // If the node should not be split, `false` should be returned, and
  // `splitInfo` is ignored.
  template<typename MatType>
  static bool SplitNode(const BoundType& bound,
                        MatType& data,
                        const size_t begin,
                        const size_t count,
                        SplitInfo& splitInfo);

  // Perform the split using the `splitInfo` object, which was populated by a
  // previous call to `SplitNode()`.  This should reorder the points in the
  // subset `data.points(begin, begin + count - 1)` such that the points for the
  // left child come first, and then the points for the right child come last.
  //
  // This should return the index of the first point that goes to the right
  // child.  This is equivalent to `begin + leftPoints` where `leftPoints` is
  // the number of points that went to the left child.  Very specifically, on
  // exit,
  //
  //   `data.cols(begin, begin + leftPoints - 1)` should contain only points
  //       that will go to the left child;
  //   `data.cols(begin + leftPoints, begin + count - 1)` should contain only
  //       points that will go to the right child;
  //   the value `begin + leftPoints` should be returned.
  //
  template<typename MatType>
  static size_t PerformSplit(MatType& data,
                             const size_t begin,
                             const size_t count,
                             const SplitInfo& splitInfo,
                             std::vector<size_t>& oldFromNew);
};

🔗 Example usage

The BinarySpaceTree class is only really necessary when a custom bound type or custom splitting strategy is intended to be used. For simpler use cases, one of the typedefs of BinarySpaceTree (such as KDTree) will suffice.

For this reason, all of the examples below explicitly specify all five template parameters of BinarySpaceTree. Writing a custom bound type and writing a custom splitting strategy are discussed in the previous sections. Each of the parameters in the examples below can be trivially changed for different behavior.

Build a BinarySpaceTree on the cloud dataset and print basic statistics about the tree.

// See https://datasets.mlpack.org/cloud.csv.
arma::mat dataset;
mlpack::data::Load("cloud.csv", dataset, true);

// Build the binary space tree with a leaf size of 10.  (This means that nodes
// are split until they contain 10 or fewer points.)
//
// The std::move() means that `dataset` will be empty after this call, and no
// data will be copied during tree building.
mlpack::BinarySpaceTree<mlpack::EuclideanDistance,
                        mlpack::EmptyStatistic,
                        arma::mat,
                        mlpack::HRectBound,
                        mlpack::MidpointSplit> tree(std::move(dataset), 10);

// Print the bounding box of the root node.
std::cout << "Bounding box of root node:" << std::endl;
for (size_t i = 0; i < tree.Bound().Dim(); ++i)
{
  std::cout << " - Dimension " << i << ": [" << tree.Bound()[i].Lo() << ", "
      << tree.Bound()[i].Hi() << "]." << std::endl;
}
std::cout << std::endl;

// Print the number of descendant points of the root, and of each of its
// children.
std::cout << "Descendant points of root:        "
    << tree.NumDescendants() << "." << std::endl;
std::cout << "Descendant points of left child:  "
    << tree.Left()->NumDescendants() << "." << std::endl;
std::cout << "Descendant points of right child: "
    << tree.Right()->NumDescendants() << "." << std::endl;
std::cout << std::endl;

// Compute the center of the BinarySpaceTree.
arma::vec center;
tree.Center(center);
std::cout << "Center of tree: " << center.t();

Build two BinarySpaceTrees on subsets of the corel dataset and compute minimum and maximum distances between different nodes in the tree.

// See https://datasets.mlpack.org/corel-histogram.csv.
arma::mat dataset;
mlpack::data::Load("corel-histogram.csv", dataset, true);

// Convenience typedef for the tree type.
using TreeType = mlpack::BinarySpaceTree<mlpack::EuclideanDistance,
                                         mlpack::EmptyStatistic,
                                         arma::mat,
                                         mlpack::HRectBound,
                                         mlpack::MidpointSplit>;

// Build trees on the first half and the second half of points.
TreeType tree1(dataset.cols(0, dataset.n_cols / 2));
TreeType tree2(dataset.cols(dataset.n_cols / 2 + 1, dataset.n_cols - 1));

// Compute the maximum distance between the trees.
std::cout << "Maximum distance between tree root nodes: "
    << tree1.MaxDistance(tree2) << "." << std::endl;

// Get the leftmost grandchild of the first tree's root---if it exists.
if (!tree1.IsLeaf() && !tree1.Child(0).IsLeaf())
{
  TreeType& node1 = tree1.Child(0).Child(0);

  // Get the rightmost grandchild of the second tree's root---if it exists.
  if (!tree2.IsLeaf() && !tree2.Child(1).IsLeaf())
  {
    TreeType& node2 = tree2.Child(1).Child(1);

    // Print the minimum and maximum distance between the nodes.
    mlpack::Range dists = node1.RangeDistance(node2);
    std::cout << "Possible distances between two grandchild nodes: ["
        << dists.Lo() << ", " << dists.Hi() << "]." << std::endl;

    // Print the minimum distance between the first node and the first
    // descendant point of the second node.
    const size_t descendantIndex = node2.Descendant(0);
    const double descendantMinDist =
        node1.MinDistance(node2.Dataset().col(descendantIndex));
    std::cout << "Minimum distance between grandchild node and descendant "
        << "point: " << descendantMinDist << "." << std::endl;

    // Which child of node2 is closer to node1?
    const size_t closerIndex = node2.GetNearestChild(node1);
    if (closerIndex == 0)
      std::cout << "The left child of node2 is closer to node1." << std::endl;
    else if (closerIndex == 1)
      std::cout << "The right child of node2 is closer to node1." << std::endl;
    else // closerIndex == 2 in this case.
      std::cout << "Both children of node2 are equally close to node1."
          << std::endl;

    // And which child of node1 is further from node2?
    const size_t furtherIndex = node1.GetFurthestChild(node2);
    if (furtherIndex == 0)
      std::cout << "The left child of node1 is further from node2."
          << std::endl;
    else if (furtherIndex == 1)
      std::cout << "The right child of node1 is further from node2."
          << std::endl;
    else // furtherIndex == 2 in this case.
      std::cout << "Both children of node1 are equally far from node2."
          << std::endl;
  }
}

Build a BinarySpaceTree on 32-bit floating point data and save it to disk.

// See https://datasets.mlpack.org/corel-histogram.csv.
arma::fmat dataset;
mlpack::data::Load("corel-histogram.csv", dataset);

// Build the BinarySpaceTree using 32-bit floating point data as the matrix
// type.  We will still use the default EmptyStatistic and EuclideanDistance
// parameters.  A leaf size of 100 is used here.
mlpack::BinarySpaceTree<mlpack::EuclideanDistance,
                        mlpack::EmptyStatistic,
                        arma::fmat,
                        mlpack::HRectBound,
                        mlpack::MidpointSplit> tree(std::move(dataset), 100);

// Save the tree to disk with the name 'tree'.
mlpack::data::Save("tree.bin", "tree", tree);

std::cout << "Saved tree with " << tree.Dataset().n_cols << " points to "
    << "'tree.bin'." << std::endl;

Load a 32-bit floating point BinarySpaceTree from disk, then traverse it manually and find the number of leaf nodes with less than 10 points.

// This assumes the tree has already been saved to 'tree.bin' (as in the example
// above).

// This convenient typedef saves us a long type name!
using TreeType = mlpack::BinarySpaceTree<mlpack::EuclideanDistance,
                                         mlpack::EmptyStatistic,
                                         arma::fmat,
                                         mlpack::HRectBound,
                                         mlpack::MidpointSplit>;

TreeType tree;
mlpack::data::Load("tree.bin", "tree", tree);
std::cout << "Tree loaded with " << tree.NumDescendants() << " points."
    << std::endl;

// Recurse in a depth-first manner.  Count both the total number of leaves, and
// the number of leaves with less than 10 points.
size_t leafCount = 0;
size_t totalLeafCount = 0;
std::stack<TreeType*> stack;
stack.push(&tree);
while (!stack.empty())
{
  TreeType* node = stack.top();
  stack.pop();

  if (node->NumPoints() < 10)
    ++leafCount;
  ++totalLeafCount;

  if (!node->IsLeaf())
  {
    stack.push(node->Left());
    stack.push(node->Right());
  }
}

// Note that it would be possible to use TreeType::SingleTreeTraverser to
// perform the recursion above, but that is more well-suited for more complex
// tasks that require pruning and other non-trivial behavior; so using a simple
// stack is the better option here.

// Print the results.
std::cout << leafCount << " out of " << totalLeafCount << " leaves have fewer "
  << "than 10 points." << std::endl;

Build a BinarySpaceTree and map between original points and new points.

// See https://datasets.mlpack.org/cloud.csv.
arma::mat dataset;
mlpack::data::Load("cloud.csv", dataset, true);

// Build the tree.
std::vector<size_t> oldFromNew, newFromOld;
mlpack::BinarySpaceTree<mlpack::EuclideanDistance,
                        mlpack::EmptyStatistic,
                        arma::mat,
                        mlpack::HRectBound,
                        mlpack::MidpointSplit> tree(
    dataset, oldFromNew, newFromOld);

// oldFromNew and newFromOld will be set to the same size as the dataset.
std::cout << "Number of points in dataset: " << dataset.n_cols << "."
    << std::endl;
std::cout << "Size of oldFromNew: " << oldFromNew.size() << "." << std::endl;
std::cout << "Size of newFromOld: " << newFromOld.size() << "." << std::endl;
std::cout << std::endl;

// See where point 42 in the tree's dataset came from.
std::cout << "Point 42 in the permuted tree's dataset:" << std::endl;
std::cout << "  " << tree.Dataset().col(42).t();
std::cout << "Was originally point " << oldFromNew[42] << ":" << std::endl;
std::cout << "  " << dataset.col(oldFromNew[42]).t();
std::cout << std::endl;

// See where point 7 in the original dataset was mapped.
std::cout << "Point 7 in original dataset:" << std::endl;
std::cout << "  " << dataset.col(7).t();
std::cout << "Mapped to point " << newFromOld[7] << ":" << std::endl;
std::cout << "  " << tree.Dataset().col(newFromOld[7]).t();